Apresentação das integrantes do grupo

Sou Ana Claudia Mota, leciono matemática para 6º e 7º anos na Escola Walter Negrelli.
Leciono há 1 ano e está sendo uma experiência ímpar.


Sou Ângela Maria Vicentim, professora de matemática há 23 anos, dos quais 18 na Escola Estadual profª Fanny Monzoni Santos. Sou apaixonada pelo que faço e tenho certeza que estou na profissão certa. Atualmente trabalho exclusivamente com o 9º ano e cada vez mais sinto necessidade de adquirir novos conhecimento para tentar entender melhor essa geração que está, aí para ser preparada para um país melhor.

Sou Ana Kelly Santos Silva, professora de matemática das 7ªs séries há 4 meses  na E.E. Profª Alice Velho Teixeira e na E.E. Major Telmo Coelho Filho. Está sendo uma experiência grandiosa.

PLANO DE AULAS

                                    

1.    TEMA→ Números

 

2.    CONTEÚDO → Equação do 2º grau.

                                         ↓

                         - Polinômios → operações

                         - Potenciação → propriedades

                         - Radiciação → propriedades e simplificação

                         - Regras de sinais

                         - Processos de resolução → soma e produto

                                                                   → fórmula de Bháskara

                                                                   → completando quadrados

                        - Sistema de equações do 2º grau

                        - História da matemática→ surgimento e desenvolvimento das  equações do 2º grau.                                   

                                                                          

 

3.    ANO/SÉRIE → 9º ano/8ª série.

 

4.    TEMPO ESTIMADO → 24 aulas

 

 

5.    JUSTIFICATIVA → O estuda das equações do 2º grau faz parte do currículo oficial e é de fundamental importância nos estudos posteriores, além das conexões com a Geometria e com situações do cotidiano.

 

6.    OBJETIVOS → Leitura e interpretações de enunciados;

               → exercitar sua capacidade de abstração;

               →Identificar uma equação do 2º grau;

               →Analisar uma situação que recai em uma equação do2º grau;

               → Reconhecer uma equação do 2º grau e seus coeficientes;

               →Verificar se um número é solução de uma equação do 2º grau;

               →Reconhecer e resolver equações do 2º grau do tipo (ax + b)² = c;

               →Compreender e aplicar a fórmula de Bháscara na resolução de equações do 2º grau, bem como por meio de completar quadrados;

               →Reconhecer e calcular equações do 2º grau incompletas.

               →Fatorar trinômios do 2º grau.

               →Resolver problemas com sistemas de equações que recaiam em equações do 2º grau.

OBS: Espera-se ao final do trabalho que os alunos sejam capazes de identificar, resolver e interpretar situações que envolvam equações do 2º grau em diferentes contextos de seu cotidiano bem como estimular a curiosidade sobre a História da Matemática.

 

7.    METAS →Atingir 75% dos alunos.

 

8.    PROCEDIMENTOS→ Pesquisar sobre o tema Equação do 2º grau: Da origem ao

                                   processo tecnológico.

                              → Discutir e tabular dados;

                              → Resolução de exercícios diversos;

                              → Resolução de problemas por métodos diversos;

                              → Incentivar o interesse em comparar métodos e                            

                                processos na resolução de problemas e elaborar estratégias de 

                                resoluções em casos mais complexos. 

                                                                                                                                        

                               → Trabalho coletivo e troca de experiências no processo de 

                                    Aprendizagem;

                               →Aulas expositivas procurando instigar a capacidade de

                                   investigação na busca de resultados, estimulando o

                                   interesse e a curiosidade para conhecer diferentes

                                   estratégias de cálculo.

 

9.    RECURSOS MATERIAIS →Apostila do aluno;

                                          → Livro Didático;

                                          → Pesquisas na internet.

OBS: considerar aspectos relevantes da pesquisa →onde pesquisar.

                                                                                 →mecanismos de busca.

                                                                                 →otimização da pesquisa.

 

10.  1. AVALIAÇÃO  →Observação direta da interação dos alunos com as atividades propostas, considerando as justificativas e as argumentações orais, bem como a produção escrita.

                    →Resolução de exercícios individualmente e coletivamente.

                    →Trabalho de pesquisa.

                    →Avaliação objetiva e com resolução de problemas.

                    →Representação com papéis coloridos através do método de completar quadrados.

10.  2. RECUPERAÇÂO → proporcionar oportunidades diferenciadas com aluno tutor em trabalhos de grupos, dando novas perspectivas de aprendizagem.

 

 GRUPO 1.

                                                    

          

                                                                       

ORIGEM DO ZERO

Embora a grande invenção prática do zero seja atribuída aos hindus, desenvolvimentos parciais ou limitados do conceito de zero são evidentes em vários outros sistemas de numeração pelo menos tão antigos quanto o sistema hindu, se não mais. Porém o efeito real de qualquer um desses passos mais antigos sobre o desenvolvimento pleno do conceito de zero - se é que de fato tiveram algum efeito - não está claro.

O sistema sexagesimal babilônico usado nos textos matemáticos e astronômicos era essencialmente um sistema posicional, ainda que o conceito de zero não estivesse plenamente desenvolvido. Muitas das tábuas babilônicas indicam apenas um espaço entre grupos de símbolos quando uma potência particular de 60 não era necessária, de maneira que as potências exatas de 60 envolvidas devem ser determinadas, em parte, pelo contexto. Nas tábuas babilônicas mais tardias (aquelas dos últimos três séculos a.C.) usava-se um símbolo para indicar uma potência ausente, mas isto só ocorria no interior de um grupo numérico e não no final. Quando os gregos prosseguiram o desenvolvimento de tabelas astronômicas, escolheram explicitamente o sistema sexagesimal babilônico para expressar suas frações, e não o sistema egípcio de frações unitárias. A subdivisão repetida de uma parte em 60 partes menores precisava que às vezes “nem uma parte” de uma unidade fosse envolvida, de modo que as tabelas de Ptolomeu no Almagesto (c.150 d.C.) incluem o símbolo 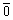ou 0 para indicar isto. Bem mais tarde, aproximadamente no ano 500, textos gregos usavam o ômicron, que é a primeira letra palavra grega oudem (“nada”). Anteriormente, o ômicron, restringia a representar o número 70, seu valor no arranjo alfabético regular.

Talvez o uso sistemático mais antigo de um símbolo para zero num sistema de valor relativo se encontre na matemática dos maias das Américas Central e do Sul. O símbolo maia do zero era usado para indicar a ausência de quaisquer unidades das várias ordens do sistema de base vinte modificado. Esse sistema era muito mais usado, provavelmente, para registrar o tempo em calendários do que para propósitos computacionais.

É possível que o mais antigo símbolo hindu para zero tenha sido o ponto negrito, que aparece no manuscrito Bakhshali, cujo conteúdo talvez remonte do século III ou IV d.C., embora alguns historiadores o localize até no século XII. Qualquer associação do pequeno círculo dos hindus, mais comuns, com o símbolo usado pelos gregos seria apenas uma conjectura.

Como a mais antiga forma do símbolo hindu era comumente usado em inscrições e manuscritos para assinalar um espaço em branco, era chamado sunya, significando “lacuna” ou “vazio”. Essa palavra entrou para o árabe como sifr, que significa “vago”. Ela foi transliterada para o latim como zephirum ou zephyrum por volta do ano 1200, mantendo-se seu som mas não seu sentido. Mudanças sucessivas dessas formas, passando inclusive por zeuero, zepiro e cifre, levaram as nossas palavras “cifra” e “zero”. O significado duplo da palavra “cifra” hoje - tanto pode se referir ao símbolo do zero como a qualquer dígito - não ocorria no original hindu.

Fonte. Tópicos de História da Matemática para uso em sala de aula; números e numerais, de Bernard GUNDLACH.

0 HOMEM VITRUVIANO DE LEONARDO DA VINCI

Conhecida imagem do Leonardo Davinci, o homem vitruviano é associado às dimensões de um homem circunscrito em um círculo e um quadrado, um ícone do ideal renascentista do homem como a medida de todas as coisas.

Largamente utilizada como representação da saúde física e mental do ser humano, esta imagem concebida por volta de 1490 refere-se originalmente aos estudos e escritos do arquiteto romano Marcus Vitruvius.

O homem vitruviano de Da Vinci, era considerado o desenho anatomicamente mais correto da sua época. Tornou-se um ícone da cultura moderna. O famoso esboço consiste em um circulo perfeito no qual um homem nu se encontra inscrito.

O homem com as pernas e braços abertos, representa um pentagrama, símbolo pré-cristão relacionado à adoração à natureza, sua interpretação mais específica, o pentagrama simboliza Vênus, a deusa do amor e da beleza.

Baseado no livro de Vitruvius Pollio, Leonardo da Vinci, criou o Homem Vitruviano, sendo este muito utilizado até os dias de hoje, pois, mostra com precisão as proporções que tem o corpo humano. No desenho, o umbigo é o centro de tudo, o homem está dentro de um círculo e um quadrado, mostrando os braços e pernas em duas posições diferentes.

Bom, melhor do que explicar é vê-lo e analisá-lo. A obra de Da Vinci está exposta na Gallerie dell'Accademia (Galeria da Academia), em Veneza, Itália, sendo esta muito importante no Renascimento Europeu. O Homem Vitruviano expõe o traçado e as proporções o corpo humano.

Especialistas afirmam que o desenho é um conceito da obra “Os dez livros da Arquitetura”, do arquiteto romano Marco Vitruvio Polião. O Homem Vitruviano mostra também o conceito da divina proporção, baseado na existência dos quatro sólidos geométricos perfeitos: o tetraedro, hexaedro, octaedro e icosaedro.

O desenho tenta expressar a beleza humana. Ele apresenta as posições dos braços e das pernas como quatro posturas diferenciadas inscritas num círculo, sendo que o umbigo é o centro da figura.

Vitrúvio já havia tentado encaixar as proporções do corpo humano dentro da figura de um quadrado e um círculo, mas suas tentativas ficaram imperfeitas. Foi apenas com Leonardo que o encaixe ficou perfeito, dentro dos padrões matemáticos esperados.

O redescobrimento das proporções matemáticas do corpo humano no século XV por Leonardo e os outros é considerado uma das grandes realizações que conduzem ao Renascimento italiano. O desenho também é considerado um símbolo da simetria básica do corpo humano e, por extensão, do universo como um todo.

É interessante também observar que a área total do círculo é idêntica à área total do quadrado (quadratura do círculo) e este desenho pode ser considerado um algoritmo matemático para calcular o valor do número irracional phi (aproximadamente 1,618).

A genialidade de Leonardo permitiu uma solução extremamente elegante. Da Vinci acreditava na perfeição da figura humana, e considerava as medidas e o funcionamento do corpo humano como uma analogia das medidas e funcionamento do universo, todas conectadas pela proporção do número de ouro dado 1,618 Phi.

O desenho é considerado um símbolo perfeito e acabado da simetria do corpo humano e um marco do antropocentrismo. Um símbolo da interconexão do homem com o universo. O estudo ficou celebrizado como o “Homem Vitruviano”, sendo aceito, como símbolo universal da humanidade.

 Este blog faz parte da formação continuada em matemática, do curso: Melhor Gestão, Melhor Ensino.

É direcionado aos professores de Matemática do Ensino Fundamental como veículo de interação e trocas de experiências no desenvolvimento das habilidades e competências.

 É fundamental ressaltar que a matemática desempenha importante papel na formação geral do indivíduo, e está relacionada a várias áreas do conhecimento, e por isso constitui uma ferramenta que deve ser amplamente explorada.

 Uma postura interdisciplinar é uma atitude de busca pelo conhecimento. Trabalhar coletivamente privilegia a interação e favorece o desenvolvimento da capacidade de argumentar e organizar informações.

Postado por Cláudia

Postado por Cláudia Soares

Postado por Cláudia, leitura e matemática: uma interação possível

Este blog é a representação das sementes lançadas pelo nosso trabalho, na esperança que possam germinar e gerar frutos na construção do conhecimento.

Há muito a disseminar neste vasto seara que é o aprendizado.

Vamos juntos buscar na matemática o seu real significado e contextualizar sua aplicação, para uma melhor leitura de mundo.